算法 网络流

网络流

Ford-Fulkerson Edmond-Karp Dinic

Posted by XDong on March 15, 2021

网络流

网络

首先，请分清楚 网络（或者流网络，Flow Network）与 网络流（Flow）的概念。

网络是指一个有向图 $G=(V,E)$。

每条边 $(u,v)\in E$ 都有一个权值 $c(u,v)$，称之为容量（Capacity），当 $(u,v)\notin E$ 时有 $c(u,v)=0$。

其中有两个特殊的点：源点（Source）$s\in V$ 和汇点（Sink）$t\in V,(s\neq t)$。

流

设 $f(u,v)$ 定义在二元组 $(u\in V,v\in V)$ 上的实数函数且满足

  1. 容量限制：对于每条边，流经该边的流量不得超过该边的容量，即，$f(u,v)\leq c(u,v)$
  2. 斜对称性：每条边的流量与其相反边的流量之和为 0，即 $f(u,v)=-f(v,u)$
  3. 流守恒性：从源点流出的流量等于汇点流入的流量，即 $\forall x\in V-{s,t},\sum_{(u,x)\in E}f(u,x)=\sum_{(x,v)\in E}f(x,v)$

那么 $f$ 称为网络 $G$ 的流函数。对于 $(u,v)\in E$，$f(u,v)$ 称为边的 流量，$c(u,v)-f(u,v)$ 称为边的 剩余容量。整个网络的流量为 $\sum_{(s,v)\in E}f(s,v)$，即 从源点发出的所有流量之和。

一般而言也可以把网络流理解为整个图的流量。而这个流量必满足上述三个性质。

注：流函数的完整定义为

\[f(u,v)=\left\lbrace\begin{aligned} &f(u,v),&(u,v)\in E\\ &-f(v,u),&(v,u)\in E\\ &0,&(u,v)\notin E,(v,u)\notin E \end{aligned}\right.\]

残量网络

首先我们介绍一下一条边的剩余容量 $c_f(u,v)$（Residual Capacity），它表示的是这条边的容量与流量之差，即 $c_f(u,v)=c(u,v)-f(u,v)$。

对于流函数 $f$，残存网络 $G_f$（Residual Network）是网络 $G$ 中所有结点 和剩余容量大于 0 的边构成的子图。形式化的定义，即 $G_f=(V_f=V,E_f=\left\lbrace(u,v)\in E,c_f(u,v)>0\right\rbrace)$。

注意，剩余容量大于 0 的边可能不在原图 $G$ 中（根据容量、剩余容量的定义以及流函数的斜对称性得到）。可以理解为，残量网络中包括了那些还剩了流量空间的边构成的图，也包括虚边（即反向边）。

增广路

在原图 $G$ 中若一条从源点到汇点的路径上所有边的 剩余容量都大于 0，这条路被称为增广路（Augmenting Path）。

或者说，在残存网络 $G_f$ 中，一条从源点到汇点的路径被称为增广路。如图：

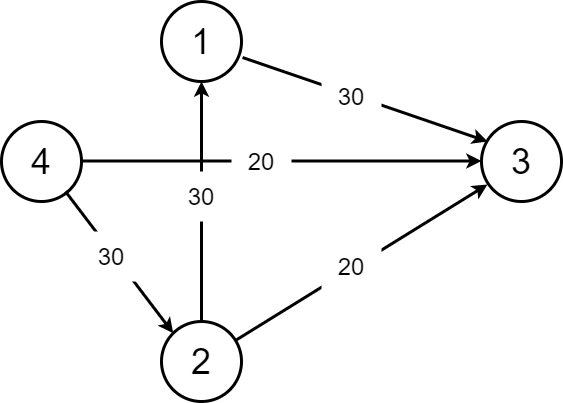
flow-1

我们从 $4$ 到 $3$，肯定可以先从流量为 $20$ 的这条边先走。那么这条边就被走掉了，不能再选，总的流量为 $20$（现在）。然后我们可以这样选择：

  1. $4\rightarrow2\rightarrow3$ 这条 增广路 的总流量为 $20$。到 $2$ 的时候还是 $30$，到 $3$ 了就只有 $20$ 了。

  2. $4\rightarrow2\rightarrow1\rightarrow3$ 这样子我们就很好的保留了 $30$ 的流量。

所以我们这张图的最大流就应该是 $20+30=50$。

反向边

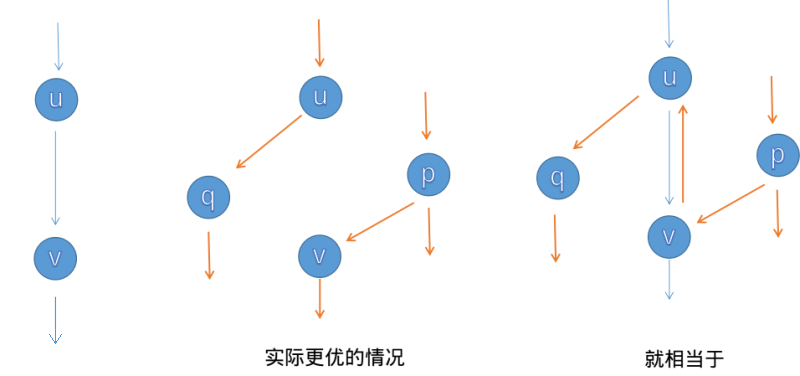
反向边理解成一种撤销，走反向边就意味着撤回上次流经正向边的若干流量，这也合理解释了为什么扣除正向边容量时要给反向边加上相应的容量：反向边的容量意味着可以撤回的量。

reverse-edge

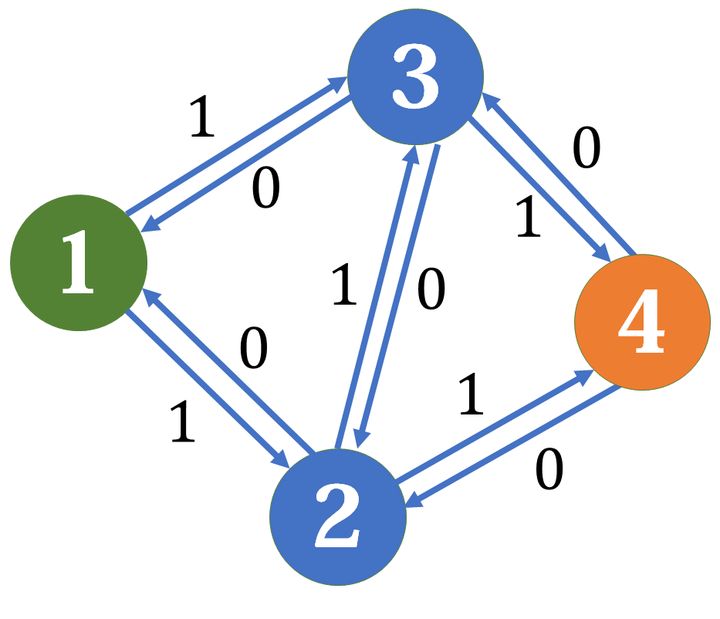
在建边的同时，在反方向建一条边权为0的边

flow-2

在扣除正向边的容量时，反向边要加上等量的容量

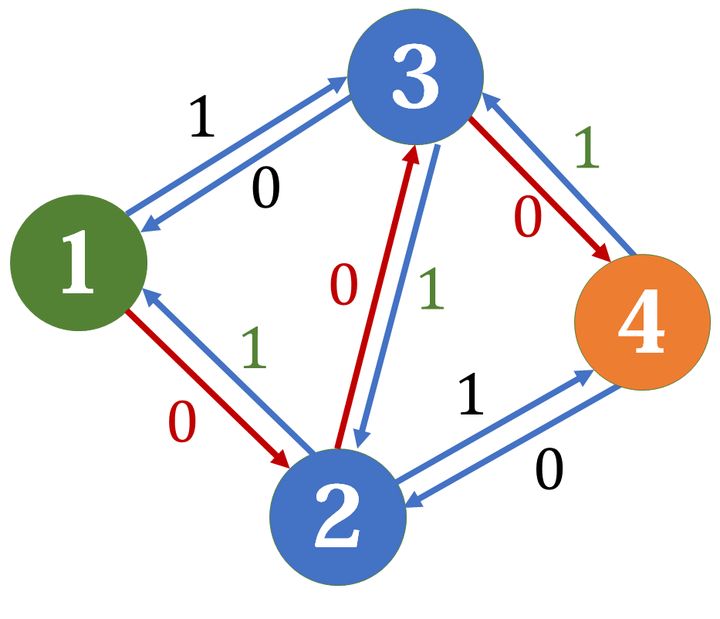
flow-3

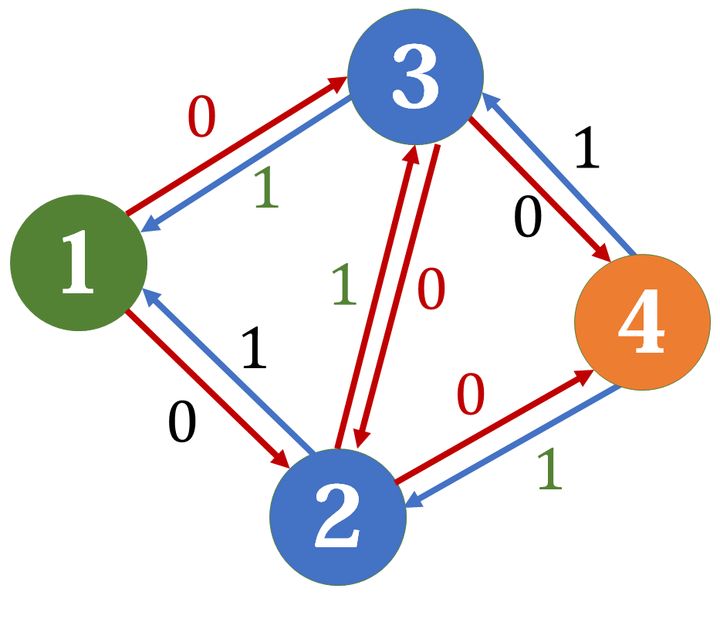
我们选择$1\rightarrow2\rightarrow3\rightarrow4$，但在扣除正向边的容量时，反向边要加上等量的容量。

这时我们可以另外找到一条增广路：$1\rightarrow3\rightarrow2\rightarrow4$。

flow-4

Ford-Fulkerson算法

即dfs找增广路，直到找不到为止

算法时间复杂度上界是$O(ef)$，其中$e$为边数，$f$为最大流

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

int n, m, s, t, cnt = 1;  // 边的下标从2开始
bool vis[MAXN];
int dfs(int p = s, int flow = INT_MAX) {
  if (p == t) {
    return flow;  // 到达终点，返回这条增广路的流量
  }

  vis[p] = true;
  for (int eg = head[p]; eg; eg = edges[eg].next) {
    int to = edges[eg].to, vol = edges[eg].cap;
    // 残余流量大于0且未访问该点
    if (vol > 0 && !vis[to]) {
      // 传递下去的流量为边的容量和当前流量中的较小值
      int c = dfs(to, min(vol, flow));
      // 可以到达终点
      if (c != -1) {
        edges[eg].cap -= c;
        edges[eg ^ 1].cap += c;
        return c;
      }
    }
  }
  
  return -1;
}

// Ford-Fulkerson算法
long long int ff() {
  long long int res = 0, c;
  while ((c = dfs()) != -1) {
    memset(vis, 0, sizeof(vis));
    res += c;
  }
  return res;
}

Edmond-Karp算法

bfs找增广路，直到找不到为止

算法时间复杂度上界是$O(ve^2)$，其中$v$为点数，$e$为边数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

int n, m, s, t, cnt = 1;  // 边的下标从2开始
int last[MAXN], flow[MAXN];  // last记录到下标点的边,last[3] = 5：到点3的为边5
                             // flow记录当前流量
int bfs() {
  memset(last, -1, sizeof(last));
  queue<int> q;
  q.push(s);
  flow[s] = INT_MAX;
  while (!q.empty()) {
    int p = q.front();
    q.pop();
    // 到达汇点，结束搜索
    if (p == t) {
      break;
    }
    for (int eg = head[p]; eg; eg = edges[eg].next) {
      int to = edges[eg].to, vol = edges[eg].cap;
      // 残余容量大于0且未访问过
      if (vol > 0 && last[to] == -1) {
        last[to] = eg;
        flow[to] = min(flow[p], vol);
        q.push(to);
      }
    }
  }
  return last[t] != -1;
}

long long int ek() {
  long long int max_flow = 0;
  while (bfs()) {
    max_flow += flow[t];
    // 从汇点原路返回更新残余容量
    for (int i = t; i != s; i = edges[last[i] ^ 1].to) {
      edges[last[i]].cap -= flow[t];
      edges[last[i] ^ 1].cap += flow[t];
    }
  }
  return max_flow;
}

Dinic算法

Dinic 算法 的过程是这样的：每次增广前，我们先用 BFS 来将图分层。设源点的层数为 $0$，那么一个点的层数便是它离源点的最近距离。

通过分层，我们可以干两件事情：

  1. 如果不存在到汇点的增广路（即汇点的层数不存在），我们即可停止增广。
  2. 确保我们找到的增广路是最短的。（原因见下文）

接下来是 DFS 找增广路的过程。

我们每次找增广路的时候，都只找比当前点层数多 $1$ 的点进行增广（这样就可以确保我们找到的增广路是最短的）。

Dinic 算法有两个优化：

  1. 多路增广：每次找到一条增广路的时候，如果残余流量没有用完怎么办呢？我们可以利用残余部分流量，再找出一条增广路。这样就可以在一次 DFS 中找出多条增广路，大大提高了算法的效率。
  2. 当前弧优化：如果一条边已经被增广过，那么它就没有可能被增广第二次。那么，我们下一次进行增广的时候，就可以不必再走那些已经被增广过的边。

算法时间复杂度上界是$O(v^2e)$，其中$v$为点数，$e$为边数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

int n, m, s, t, cnt = 1;  // 边的下标从2开始
int lv[MAXN], cur[MAXN];  // lv是每个点的层数
                          // cur用于当前弧优化标记增广起点
// bfs分层
bool bfs() {
  memset(lv, -1, sizeof(lv));
  lv[s] = 0;
  memcpy(cur, head, sizeof(head));  // 当前弧优化初始化
  queue<int> q;
  q.push(s);
  while (!q.empty()) {
    int p = q.front();
    q.pop();
    for (int eg = head[p]; eg; eg = edges[eg].next) {
      int to = edges[eg].to, vol = edges[eg].cap;
      if (vol > 0 && lv[to] == -1) {
        lv[to] = lv[p] + 1;
        q.push(to);
      }
    }
  }
  return lv[t] != -1;  // 如果汇点未访问过说明无法到达
}

int dfs(int p = s, int flow = INT_MAX) {
  if (p == t) {
    return flow;
  }
  int rmn = flow;
  for (int eg = cur[p]; eg && rmn; eg = edges[eg].next) {
    cur[p] = eg;  // 当前弧优化 当走到第i条弧时，前面i-1条弧已经流满了
    int to = edges[eg].to, vol = edges[eg].cap;
    // 往层数高的方向增广
    if (vol > 0 && lv[to] == lv[p] + 1) {
      int c = dfs(to, min(vol, rmn));  // 尽可能多地传递流量
      rmn -= c;  // 剩余流量减小
      edges[eg].cap -= c;  // 更新残余容量
      edges[eg ^ 1].cap += c;
    }
  }
  return flow - rmn;  // 返回传递出去的流量的大小
}

long long dinic() {
  long long int res = 0;
  while (bfs()) {
    res += dfs();
  }
  return res;
}

网络最大流

网络流模板题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

#include <bits/stdc++.h>
#define IO ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
const int MAXN = 205;

struct edge {
  int to;
  int cap;
  int next;
} edges[10005];
int head[MAXN];

int n, m, s, t, cnt = 1;  // 边的下标从2开始
int lv[MAXN], cur[MAXN];  // lv是每个点的层数
                          // cur用于当前弧优化标记增广起点
// bfs分层
bool bfs() {
  memset(lv, -1, sizeof(lv));
  lv[s] = 0;
  memcpy(cur, head, sizeof(head));  // 当前弧优化初始化
  queue<int> q;
  q.push(s);
  while (!q.empty()) {
    int p = q.front();
    q.pop();
    for (int eg = head[p]; eg; eg = edges[eg].next) {
      int to = edges[eg].to, vol = edges[eg].cap;
      if (vol > 0 && lv[to] == -1) {
        lv[to] = lv[p] + 1;
        q.push(to);
      }
    }
  }
  return lv[t] != -1;  // 如果汇点未访问过说明无法到达
}

int dfs(int p = s, int flow = INT_MAX) {
  if (p == t) {
    return flow;
  }
  int rmn = flow;
  for (int eg = cur[p]; eg && rmn; eg = edges[eg].next) {
    cur[p] = eg;  // 当前弧优化 当走到第i条弧时，前面i-1条弧已经流满了
    int to = edges[eg].to, vol = edges[eg].cap;
    // 往层数高的方向增广
    if (vol > 0 && lv[to] == lv[p] + 1) {
      int c = dfs(to, min(vol, rmn));  // 尽可能多地传递流量
      rmn -= c;  // 剩余流量减小
      edges[eg].cap -= c;  // 更新残余容量
      edges[eg ^ 1].cap += c;
    }
  }
  return flow - rmn;  // 返回传递出去的流量的大小
}

long long dinic() {
  long long int res = 0;
  while (bfs()) {
    res += dfs();
  }
  return res;
}

void add_edge(int u, int v, int w) {
  edges[++cnt].to = v;
  edges[cnt].cap = w;
  // 链表头插法
  edges[cnt].next = head[u];
  head[u] = cnt;
}

int main() {
  IO;
  cin >> n >> m >> s >> t;
  int u, v, w;
  for (int i = 0; i < m; i++) {
    cin >> u >> v >> w;
    add_edge(u, v, w);
    add_edge(v, u, 0);  // 反向边
  }
  cout << dinic();
  return 0;
}

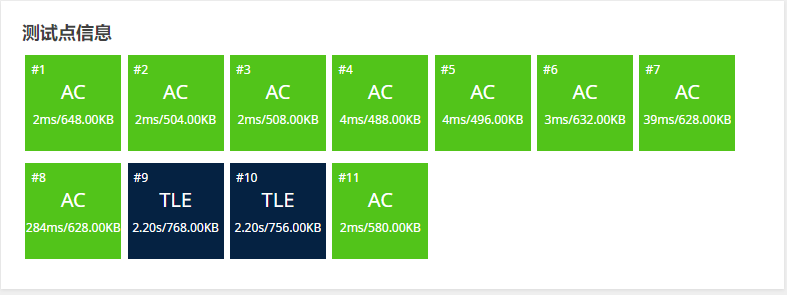
不同算法时间对比

  • Ford-Fulkerson Ford-Fulkerson

  • Edmond-Karp Edmond-Karp

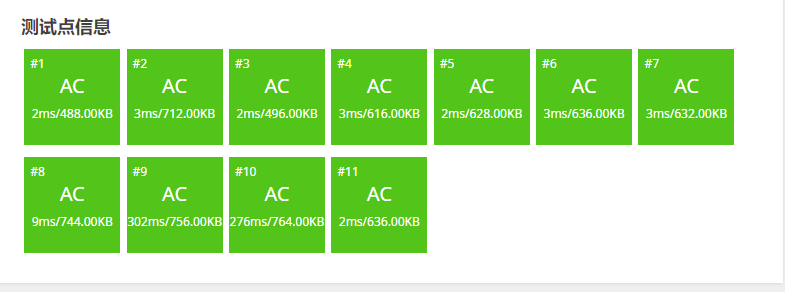
  • Dinic Dinic

参考链接

CATALOG
    FEATURED TAGS
    算法 复习 数据结构 Codeforces 学习 嵌入式 并查集 搜索
    FRIENDS